Dead Reckoning Meets Radar Odometry
Table of Links
Abstract and I. Introduction
II. Related Works
III. Dead Reckoning using Radar Odometry
IV. Stochastic Cloning Indirect Extended Kalman Filter
V. Experiments
VI. Conclusion and References
II. RELATED WORKS
A. Dead Reckoning
\ The DR method has been extensively researched and popularly adopted as a straightforward and computationally effecient solution for odometer/INS/GNSS integrated system in GNSS-denied environments [15]–[17]. Simulation and field test results have consistently shown the effectiveness of this approach over the conventional INS-based system [13], [18]. To further improve its robustness, adaptive rules for the Extended Kalman Filter (EKF) were introduced by [19] to handle measurement outliers and dynamic model disturbances. In addition, Takeyama et al. [20] extended the traditional DR-based structure by incorporating a monocular camera to improve heading estimation accuracy.
\ Concurrently, many researchers have focused on improving odometer quality by estimating and compensating for the odometer’s scale factor [21]. Park et al. [13] addressed nonholomic constraints of the wheeled vehicle to suspend the odometer side-slip errors. The authors also utilized tilt angles calculated from gravitational force measurements to further enhance roll and pitch angles estimation. The same approach was also explored in [17].
\ One thing we notice from these previous researches is that, most of the DR-based application has primarily been applied to land vehicles, with limited extensions to other platforms such as drones. This restriction stems from the availability of odometers in wheeled vehicles, their costeffectiveness, and they require minimal effort to compute the vehicle’s body velocity. Moreover, it is not straightforward to directly measurement body velocity in other non-wheeled applications. In contrast to previous approaches, our work employs a 4D FMCW radar instead of an odometer, thus overcoming this limitation.
\ B. Radar Inertial Odometry
\ According to [8], one of the earliest contributions to radar inertial odometry is the EKF RIO [11] introduced by Doer and Trommer. The key achievement was the expansion of previous research on 2D radar odometry with motion constraints into the realm of 3D. Specifically, they integrated inertial data from IMUs with 3D radar-based ego velocity estimates using EKF framework. Additionally, 3-point Random sample consensus (RANSAC) estimator has been applied to deal with radar noisy point clouds. This impressive results formed the foundation for their subsequent studies in this field. In [22], they employed stochastic cloning technique to estimate the IMU-radar extrinsic calibration matrix, further refining the accuracy of the EKF RIO. Next, they introduced a novel method for calculating the relative heading angle from radar ranges measurement under Manhattan world assumptions [23]. Expanding on their work, in [24], Doer and Trommer extended the RIO pipeline by incorporating both monocular and thermal cameras to tackle extremely challenging visual conditions. Recently, they have further enhanced the system by adding a GNSS receiver [25]. Ng et al. [26] proposed a continuous-time framework for fusing an IMU with multiple heterogeneous and asynchronous radars.
\ In contrast to the Doppler-based approaches mentioned above, where only a single radar scan is utilized, the technique of calculating relative pose between two scans via scan matching is less favored due to the sparsity and noise nature of radar measurements. Michalczyk et al. [27] presented a hybrid method that update the estimation by leveraging both ego velocity measurement and matched 3D points obtained from scan matching using stochastic cloning technique [28]. In [29], they introduced a novel persistent landmarks concept, which serves to increase the accuracy of scan matching. Almalioglu et al. [30] used Normal Distributions Transform (NDT) to determine the optimal transformation between corresponding points in consecutive radar scans. Subsequently, this measurement was integrated into the EKF RIO without incorporating Doppler velocity measurements.
\ Despite the utilization of radar measurements, radar remained classified as an assisted sensor in the aforementioned studies. Our approach, on the other hand, considers radar as both the primary sensor and an aided sensor concurrently. Particularly, Doppler-based measurement will primarily be used for position calculation, while range measurements will serve to update the estimation. A key motivation behind this configuration is the superior accuracy of velocity estimates derived from radar compared to those from an IMU, especially in high dynamic motions. As a result, in the conventional framework, such as RIO, the velocity estimate provided by the INS typically converges towards the velocity estimate derived from radar.
\
III. DEAD RECKONING USING RADAR ODOMETRY
A. Coordinate Frame and Mathematical Notations

B. System Overview

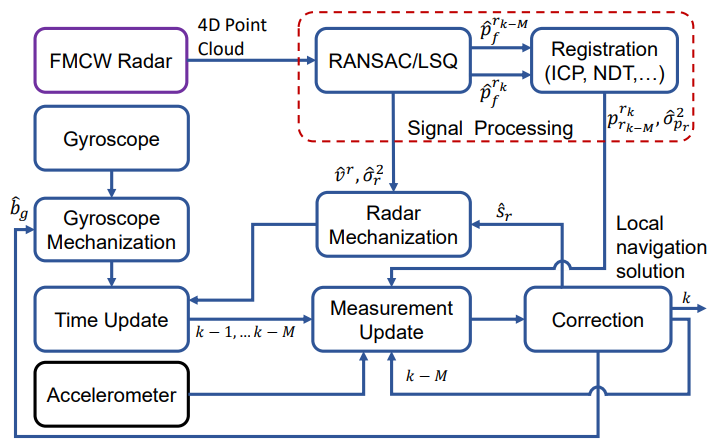
It is important to note that we operate under the assumption of a static environment. In other words, throughout the entire process, no moving objects are present within the field of view (FOV) of the radar. Chen et al. [31] have demonstrated that the accuracy of ego velocity estimation from radar degrades rapidly in the presence of moving objects within the scene. However, addressing this issue falls outside the scope of this article.
\ C. Radar mechanization

Since radar velocity measurement is used to calculate the localization information, we transform (1) as follows
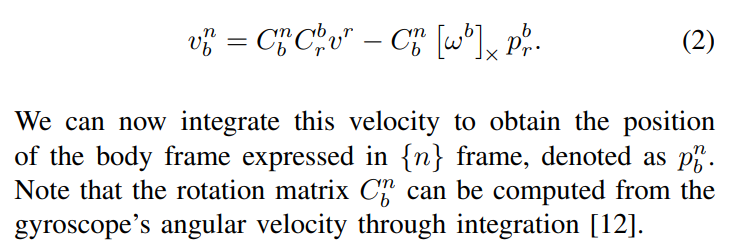
\
:::info Authors:
(1) Hoang Viet Do, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]);
(2) Yong Hun Kim, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]);
(3) Joo Han Lee, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]);
(4) Min Ho Lee, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected])r;
(5) Jin Woo Song, Intelligent Navigation and Control Systems Laboratory (iNCSL), School of Intelligent Mechatronics Engineering, and the Department of Convergence Engineering for Intelligent Drone, Sejong University, Seoul 05006, Republic Of Korea ([email protected]).
:::
:::info This paper is available on arxiv under ATTRIBUTION-NONCOMMERCIAL-NODERIVS 4.0 INTERNATIONAL license.
:::
\
You May Also Like

What a Digital Euro on Ethereum or Solana Means for Europe’s Monetary Sovereignty

Kristin Johnson Resigns as CFTC Commissioner Amid Regulatory Uncertainty
