The Simple River Measurement That Predicts Ecosystem Collapse
Table of Links
Abstract and 1. Introduction
-
The well-posed global solution
-
Nontrivial stationary solution
3.1 Spectral theory of integro-differential operator
3.2 The existence, uniqueness and stability of nontrivial stationary solution
-
The sharp criteria for persistence or extinction
-
The limiting behaviors of solutions with respect to advection
-
Numerical simulations
-
Discussion, Statements and Declarations, Acknowledgement, and References
5 The limiting behaviors of solutions with respect to advection


\ 
\ 
\ 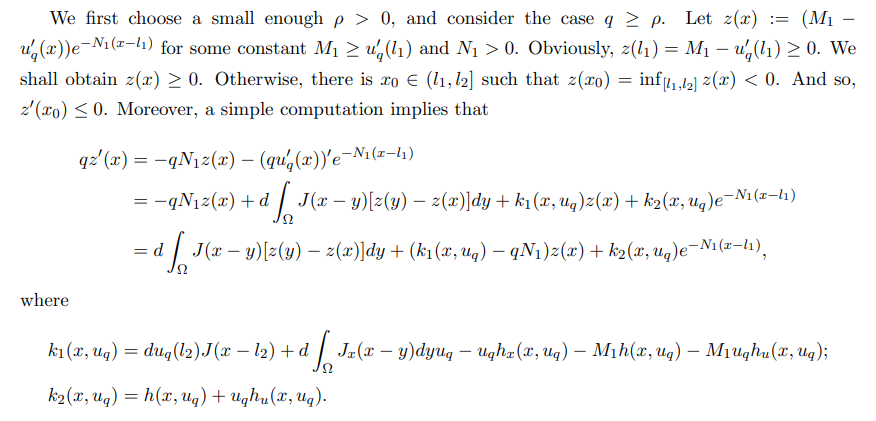
\ 
\ 
\ It follows that uq(x) is equi-continuous in q ∈ [0, ρ].
\ 
\ According to [32], the above equation has a unique positive solution for all d > 0.
\ 
\ 
\ 
\ 
\ The proof is completed.
\ Remark 5.5. Note that γ(x) is the unique nontrivial stationary solution of (5.3).
\ Similarly, for (1.4), we have
\ 
\
6 Numerical simulations

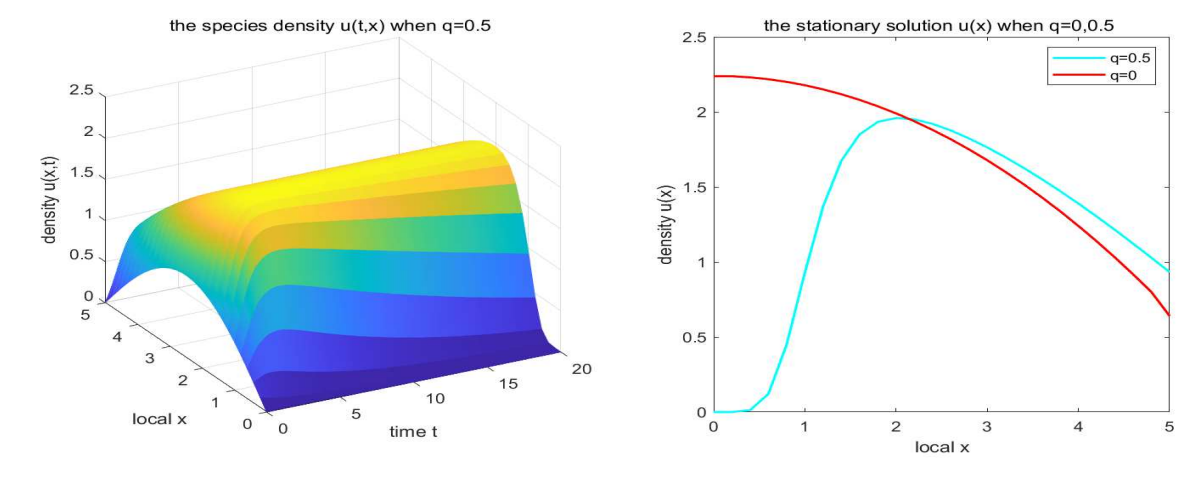
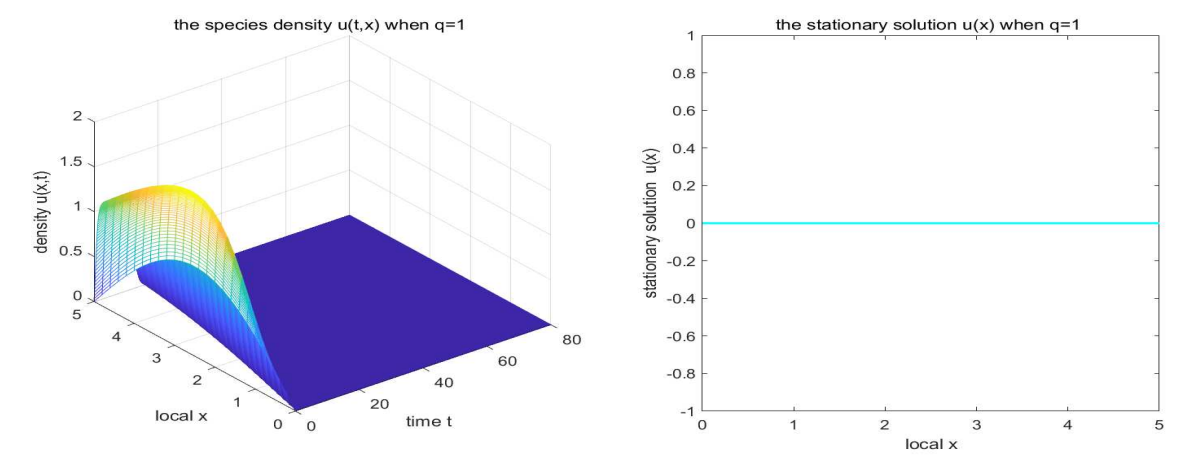
\ Example 1. A numerical sample for case q = 0.5 is presented in Fig. 1. We observe that species u will ultimately survive and its species density reaches a steady state as time tends to infinite in domain Ω = (0, 5). And from Fig. 1, we find that the advection rate has an impact on the steady state of species density. A numerical sample for case q = 1 is shown in Fig. 2. It follows that species u will extinct in domain Ω = (0, 5), which implies that its species density will tend to 0 as time tends to infinite. Then Figs. 1 and 2 depict the temporal dynamics of species u for system (1.4).
\ 
\ 
\ 
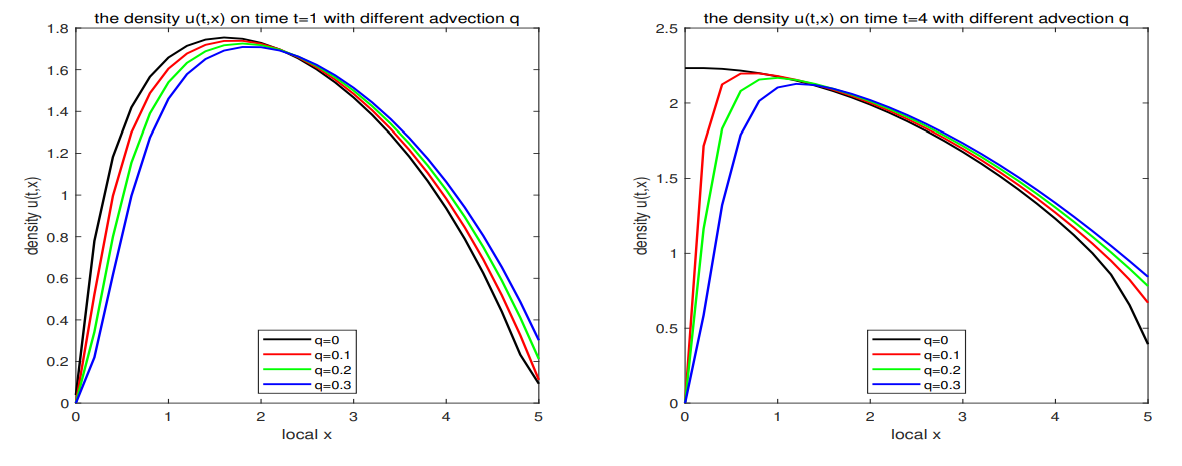
\ Example 2. Choosing q = 0, 0.1, 0.2, 0.3, by Theorem 4.2, the species will survive and has a steady-state. Figs. 4 and 5 describe the profiles of u with different q at time t = 1, 4 and the profiles of u with different q at location x = 1, 4. We find that when the advection rate has a tendency to 0, the species density will close to the species density for q = 0. Meanwhile, Fig. 6 shows that the stationary solution will close to the stationary solution for q = 0 when the advection rate q tends to 0. These phenomena explain our results for Theorems 5.6 and 5.7 with q → 0 +.
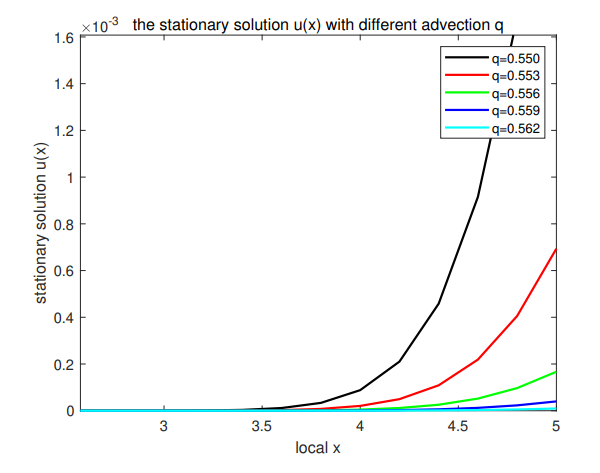
\ Example 3. By choosing q = 2, 4, 6, 8, we get the profiles of u with different q at time t = 1, 1.2 and the profiles of u with different q at location x = 1, 4; see Figs. 7 and 8. We find that when the advection rate q becomes large, the species density will have a tendency to 0 for any time and location, which explain the result of Theorem 5.7 with q → ∞.
\ 
\ 
\
:::info Authors:
(1) Yaobin Tang, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China;
(2) Binxiang Dai, School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha, Hunan 410083, P. R. China ([email protected]).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
You May Also Like

Portuguese fugitive Pedro M., accused of €500 million ($586 million) crypto and credit card fraud
Tether Expands into Gold with $200M Tokenized Treasury Plan
